[알고리즘 특강] 2. Tree

September 16, 2024 5 분 소요

1. 트리의 정의와 필요성

1.1 트리란?

정의: 한 노드가 여러 노드를 가리킬 수 있는 비선형적 자료구조
특징:
- 최상위 노드가 존재하는 계층적 형태
- 그래프 자료구조 중 하나인 단방향 그래프
- 시작노드에서 출발해 다시 돌아올 수 없는 사이클이 없는 연결 그래프

1.2 트리의 활용

우리가 흔히 볼 수 있는 트리 중 하나는 파일 탐색기

최상위 폴더 > 하위 폴더 > 파위 폴더, 파일 등

2. 트리 구조와 용어

2.1 트리의 기본 구조

Tree

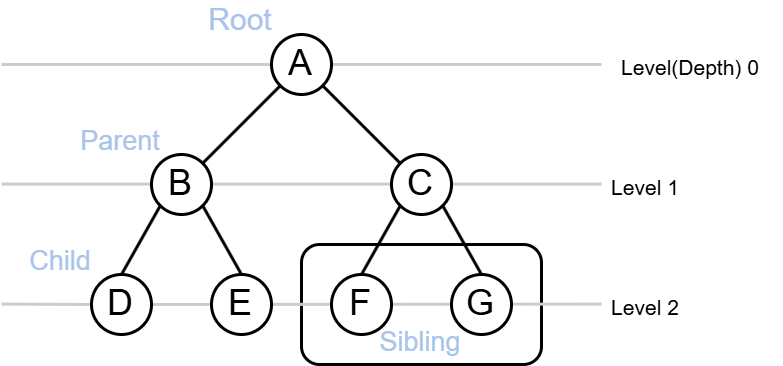
2.2 트리의 주요 용어

노드 (Node): 트리를 구성하는 데이터 원소
간선 (Edge): 노드와 노드를 연결하는 선 (노드의 개수 n, 간선의 수 n-1)
루트 노드 (Root Node): 부모 노드가 없는 트리의 최상단 노드, 트리에 1개만 존재
부모 노드 (Parent Node): 연결된 두 노드 중 위에 있는 노드
자식 노드 (Child Node): 부모 노드의 하위 노드
형제 노드 (Sibling Node): 같은 부모의 자식 노드들
조상 노드 (Ancestor Node) / 자손노드 (Descendent Node): 노드 V에서 부모 노드로만 계속 이동해서 노드 U로 갈 수 있다면 U는 V의 조상 노드, V는 U의 자손 노드
리프 노드 (Leaf Node): 자식 노드가 없는 노드
서브 트리 (Sub Tree): 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
높이 (Height): 리프노드에서 해당 노드까지 이동하기 위해 거치는 간선의 수
깊이 (Depth): 루트 노드부터 해당 노드까지 이동하기 위해 거치는 간선의 수
레벨 (Level): 같은 깊이를 가진 노드의 집합
트리의 크기 (Size of Tree): 노드의 개수와 동일

3. Binary Search Tree(BST)

3.1 BST의 특징

BST

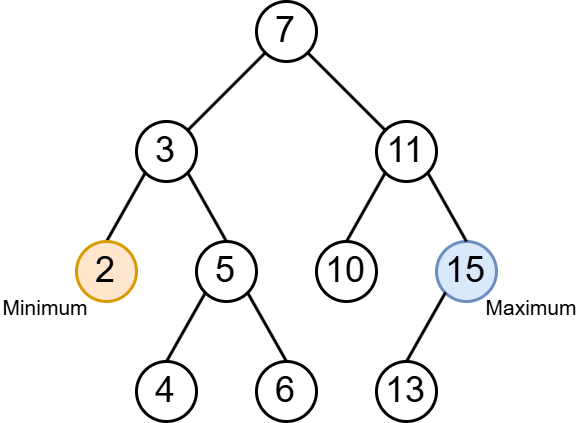
원소의 중복을 허용하지 않음
노드의 왼쪽 서브 트리는 노드 값보다 작은 값을 가짐
노드의 오른쪽 서브 트리는 노드 값보다 큰 값을 가짐

이런 특성으로 BST에서:

최솟값은 트리 레벨에 관계없이, 가장 왼쪽 끝에 위치한 노드
최댓값은 가장 오른쪽 끝에 있는 노드
C++ set에는 Binary Search Tree중 하나인 Red Black Tree가 사용됨

4. Binary Search Tree 구현

4.1 초기화

struct Node {
	int key;
	Node *left, *right;
}

constexpr size_t MAX_NODE = 1000; //정적 할당 방식

int node_count = 0;
Node node_pool[Max_NODE];

Node* new_node(int x) {
	node_pool[node_count].key = x;
	node_pool[node_count].left = nullptr;
	node_pool[node_count].right = nullptr;
	
	return &node_pool[node_count++];
}

Node* root; // 루트 노드를 가리키는 포인터

void init() { // init함수 호출 시 루트 노드를 NULL로 초기화, 트리에 노드가 없는 상태
	root = nullptr;
	node_count = 0;
}

4.2 삽입

void insert(int x) {
	root = insert_rec(root, x);
}

Node* insert_rec(Node* node, int x) {
	if (node == nullptr){
		return new_node(x);
	}
	
	if (x < node->key) {
		node->left = insert_rec(node->left, x);
	}
	else if (x > node->key) {
		node->right = insert_rec(node->right, x);
	}
	return node;
}

4.3 삽입 동작 과정

재귀로 구현한 노드의 삽입 Node* insert_rec(Node* node, int x) 함수는 node를 루트로 하는 서브트리에 x를 삽입한 다음 서브 트리의 루트를 리턴하는 함수이다. 동작 과정을 3개 케이스로 나눠서 이해해보자:

Node = NULL인 경우
- 서브트리가 비어있는 경우
- X를 추가해주면 노드가 x하나뿐인 서브 트리가 생기므로 x 노드를 만든 뒤 바로 리턴
Node의 왼쪽 자식에 x가 들어가야 하는 경우(x < node->key)
- 왼쪽 서브 트리에 x를 삽입한 뒤 왼쪽 서브 트리의 루트를 왼쪽 자식으로 만듦
- insert_rec함수를 그대로 사용하여 재귀적으로 풀 수 있음
- 자식의 서브트리에 노드를 삽입해도 루트는 변하지 않으므로 node를 그대로 리턴
Node의 key와 x가 같은 경우
- 이미 트리에 x가 존재하는 경우
- Binary Search Tree는 원소의 중복을 허용하지 않으므로 아무것도 하지않고 node를 그대로 리턴

4.4 삭제

void remove(int x) {
	root = remove_rec(root, x);
}

int find_min_key(Node* node) {
	while (node->left !=nullptr){
		node = node->left;
	}
	return node->key;
}

Node* remove_rec (Node* node, int x) {
	if (node==nullptr) return node;
	
	if (x < node->key) {
		node->left = remove_rec(node->left, x);
	}
	if (x < node->key) {
		node->right = remove_rec(node->right, x);
	}
	else {
		if (node->left == nullptr) return node->right;
		else if (node->right == nullptr) return node->left;
        
        const int temp = find_min_key(node->right);
        node->key = temp;
        node->right = remove_rec(node->right, temp);
	}
    return node;
}

4.5 삭제 동작 과정

삽입과 비슷하다. Node* remove_rec(Node* node, int x) 함수는 node를 루트로 하는 서브트리에 x를 삭제한 다음 서브트리의 루트를 리턴하는 함수이다. 3가지 경우로 나눠서 이해해보자:

Node = NULL인 경우
- x가 원래 트리에 없는 경우
- 아무 것도 하지 않고 서브 트리의(NULL)을 리턴
Node의 왼쪽 자식에서 x를 삭제해야 하는 경우(x < node->key)
- 왼쪽 서브트리에서 x를 삭제한 다음 왼쪽 자식을 그 서브 트리의 루트로 바꿔줌
- 삽입과 마찬가지로 재귀적으로 풀 수 있음
Node의 key와 x가 같은 경우
- node를 삭제해야 함
- node를 삭제하고 node의 부모 노드와 node의 자식 노드를 트리 구조에 맞게 이어줌
- 두 가지 경우로 나뉨:
  1. Node의 한 쪽 자식이 없는 경우
    - 노드를 삭제해도 됨
    - 트리를 1.루트 2.왼쪽 서브 트리 3. 오른쪽 서브 트리로 나눌 수 있음
    - 루트 노드는 지금 삭제할 것이고, 한쪽 서브 트리는 이미 없으니 나머지 하나의 서브 트리만 남음
    - 그 서브 트리가 원래의 트리를 대체하게 됨
  2. Node에게 왼쪽 자식, 오른쪽 자식 모두 있는 경우
    - node를 삭제하고 그자리에 왼쪽, 오른쪽 중 어떤게 와야하는가?
    - 둘다 안됨
    - Binary Search Tree 구조를 유지하기 위해 node 자리에는 node의 왼쪽 서브 트리의 모든 값보다 크고, node의 오른쪽 서브 트리의 모든 값보다 작은 값이 와야 함
    - 이를 위해서 node의 key를 오른쪽 서브트리에서 가장 작은 key 값으로 바꾸고, 오른쪽 서브트리에서 그 key를 대신 삭제하는 대안을 사용
    - (왼쪽 서브트리에서 가장 큰 key값을 찾아도 됨)

4.6 탐색

bool find(int x) {
    Node* node = root;
    while (node != nullptr) {
        if (node->key == x){
            return true;
        }
        node = x < node->key ? node->left : node->right;
    }
    return false;
}

5. 트리 순회

5.1 순회의 종류

Binary Tree를 순회하는 방법에는 크게 3가지가 있다:

pre-order (전위 순회)
- 자신 -> 왼쪽 서브 트리 -> 오른쪽 서브 트리 순서로 방문
- pre-order 방문 순서는 위상 정렬 결과와 같음
in-order (중위 순위)
- 왼쪽 서브 트리 -> 자신 -> 오른쪽 서브 트리 순서로 방문
- Binary Search Tree에서 in-order 방문 순서는 key를 정렬한 결과와 같음
post-order (후위 순위)
- 왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 자신 순서로 방문
- post-order 순회는 자식 서브 트리를 모두 방문한 후에 자신을 방문하므로 자식 노드에서 계산된 결과를 자신이 활용할 수 있음
- 이를 활용한 대표적인 예로 계산기 구현, 세그먼트 트리가 있음

위의 순회 방법은 재귀 호출 단계에서 자신을 언제 호출하느냐에 따라 간단히 구현할 수 있음

5.2 순회 구현 (재귀)

// 순회 (type: 0 전위,  1 중위,  2 후위)
void traversal(int type) const {
    static constexpr array< const char*, 3> traversal_types = { "pre","in","post"};
    cout << traversal_types[type] << "-order";
    traversal_rec(root, type);
    cout << "\n";
}

void traversal_rec(Node* node) const {
    if (node == nullptr ) return;
    // if (type == 0) cout << node->key << ' '; // pre-order
    traversal_rec(node->left, type);
    // if (type == 1) cout << node->key << ' '; // in-order
    traversal_rec(node->right, type);
    // if (type == 2) cout << node->key << ' '; // post-order
}

5.3 순회 구현 (비재귀)

// 스택을 사용한 트리 순회 (pre-order)
using namespace std;

void pre_order() {
	stack <Node*> stk;
    stk.emplace(root)
       
    cout << "pre-order ";
    while (!stk.empty()) {
        const Node* node = stk.top()
        stk.pop()

        cout << node->key << '';

        if (node->right != nullptr)  stk.emplace(node->right);
        if (node->left != nullptr)   stk.emplace(node->left);
    }
    cout << '\n';
}
// in-order, post-order도 스택으로 구현

6. Self-Balanced Binary Search Tree

6.1 높이 계산

높이가 H인 트리에 노드를 최대한 넣으면 2^(H+1)-1
N <= 2^(H+1) - 1
log2N -1<= H

6.2 종류

Red-Black Tree
Splay Tree
B-Tree

Twitter Facebook LinkedIn

Baymax