[알고리즘 특강] 3. Union Find

1. Union-Find의 정의와 필요성

1.1 Union-Find란?

• 정의: 상호 배타적 집합(서로소 집합)(Disjoint-Set)을 표현할 때 사용하는 그래프 알고리즘
• 역할: 임의의 두 노드(원소)가 서로 같은 그래프(집합)에 속하는지 판별하는 알고리즘
• 구현: 집합을 트리 구조를 이용하여 구현

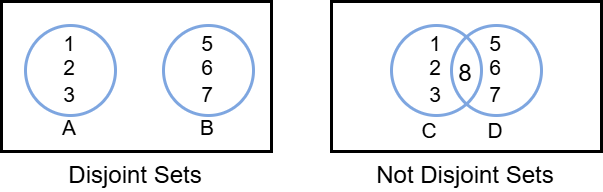
1.2 Disjoint-Set이란?

• 정의: 공통원소가 없는 “상호 배타적인” 부분집합들로 나눠진 원소들에 대한 정보를 표현하는 자료구조
• 주요 연산:
  • Union (합치기): 두 원소가 속한 집합을 하나로 합침
  • Find(찾기): 해당 원소가 속한 집합을 반환

2. Union-Find의 동작 원리

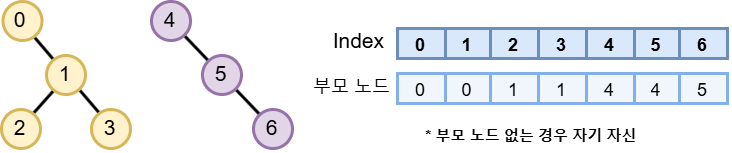
2.1 기본 원리

이 알고리즘의 핵심은 각각의 집합을 트리로 나타내는 것이다. Union-Find를 사용하면 특정 노드가 어느 집단에 속해 있는지 알 수 있다.

2.2 시간복잡도

• 트리의 구조를 사용해서 시간복잡도가 평균적으로 O(log N)
• 편향될 경우 O(N)이 될 수 있음
• 경로 압축 (Path Compression), Rank기반 연산을 통해 최적화하여 상수에 가깝게 만들 수 있음

3. Union-Find 구현

3.1 초기화

parent[x] = x가 속한 집합의 번호 (자기자신)으로 초기화

int parent[MAX_SIZE];

void initialize() {
	for(int x=0; x < MAX_SIZE; x++)
		parent[x] = x;
}

3.2 Find 연산

Node x의 Root를 찾음 부모 노드가 자기 자신일 때까지 타고 올라감 (재귀 함수)

int Find(int x) {
	if( x == parent[x] )
		return x;
	else
		return Find(parent[x]);
}

3.3 Union 연산

Node a와 Node b를 합침 b의 root의 부모를 a의 root로 연결

void Union(int a, int b) {
	int A = Find(a); // root of a
	int B = Find(b); // root of b
	
	parent[B] = A;
}

4. Union-Find 최적화

4.1 Path Compression

Find에서 root를 찾는 경우 최악의 상황에서 O(N) 만큼의 계산 요구

예시:

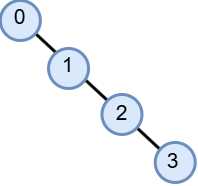
Find(3)의 경우 모든 노드 탐색 요구

-> 경로 압축 방법(Path Compression)이 필요

Find는 Depth가 낮을 수록 유리함 -> 매번 Find할 때 Depth가 2 이상이면 Path compression 수행

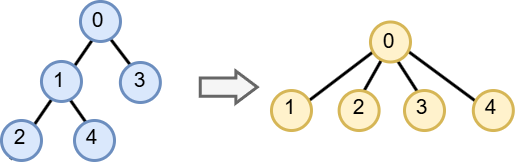
Path Compression 수행 시 Find에 대한 계산 복잡도 단축 특징: Root node를 원하는 값으로 강제할 수 있음

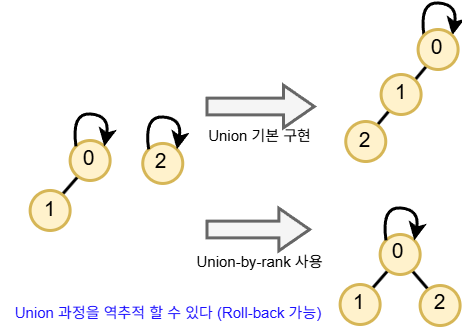
4.2 Union-by-rank

rank에 트리의 높이(rank)를 저장 항상 높이(rank)가 더 낮은 트리를 높은 트리 밑에 넣음

void Union(int a, int b) {
	int A = Find(a); // root of a
	int B = Find(b); // root of b
	
	if (A==B)
		return;
	if(rank[A] < rank[B]) 
		parent[A] = B;
	else if (rank[A] > rank[B])
		parent[B] = A;
	else {	// rank[A] == rank[B]
		parent[B] = A;
		rank[A]++;
	}  
}